散布図の確認
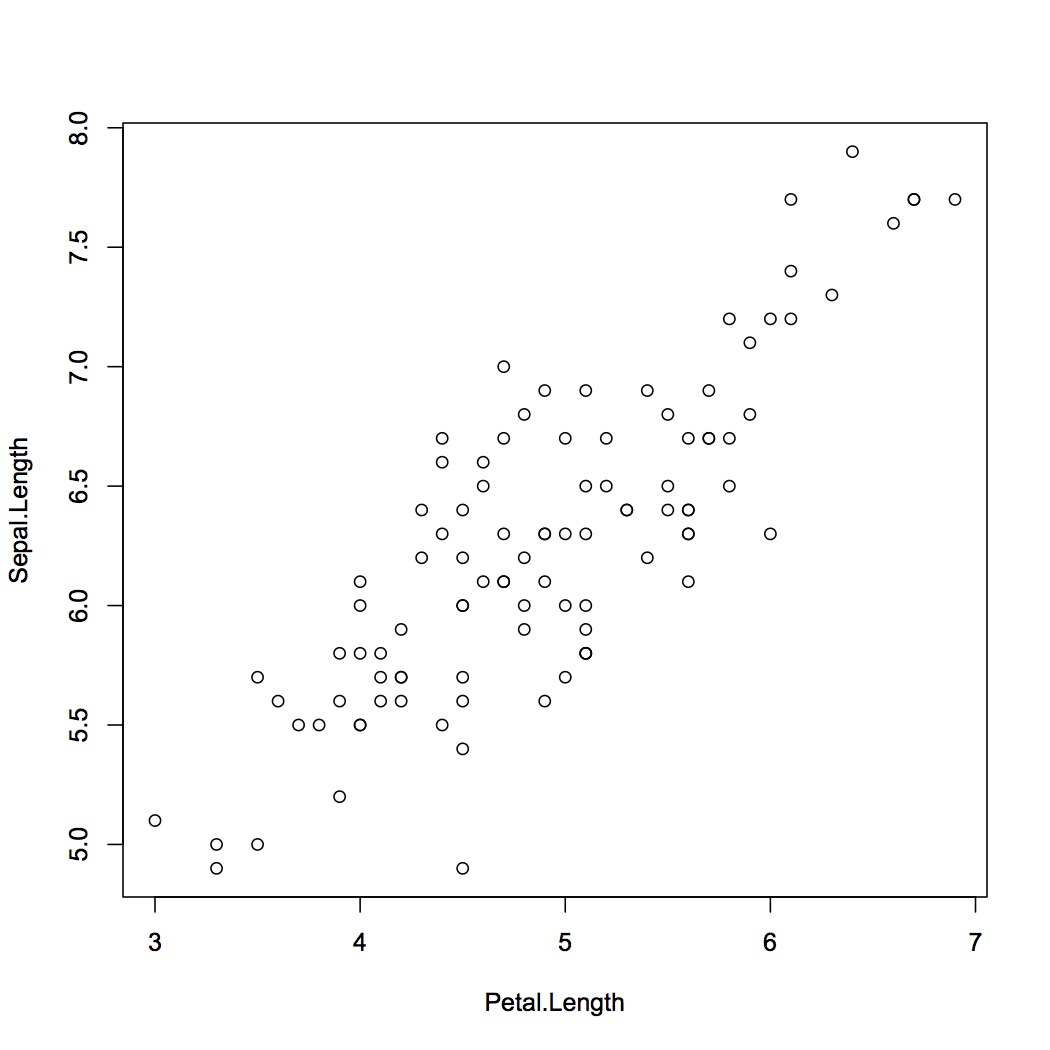
irisのデータを見ていると、verisicolorとvirginicaはPetal.LengthとSepal.Lengthに相関関係がありそうだ。 詳細に確認するため、irisのデータからsetosaを除いてプロットする。
> iris.new <- subset(iris, Species!="setosa")
> plot(Sepal.Length~Petal.Length, data=iris.new)
線形モデルにフィットさせる
線形モデルにフィットさせるにはlm()関数を使用する。
lm(formula, deta)
| 引数 | 説明 |
|---|---|
| formula | フォーミュラクラスのオブジェクト |
| data | 使用するデータフレーム |
> iris.mdl <- lm(formula=Sepal.Length~Petal.Length, data=iris.new)
回帰分析の結果を表示する
回帰分析の結果をsummary()関数を用いて、確認してみる。
> summary(iris.mdl)
Call:
lm(formula = Sepal.Length ~ Petal.Length, data = iris.new)
Residuals:
Min 1Q Median 3Q Max
-1.09194 -0.26570 0.00761 0.21902 0.87502
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.99871 0.22593 13.27 <2e-16 ***
Petal.Length 0.66516 0.04542 14.64 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.3731 on 98 degrees of freedom
Multiple R-squared: 0.6864, Adjusted R-squared: 0.6832
F-statistic: 214.5 on 1 and 98 DF, p-value: < 2.2e-16
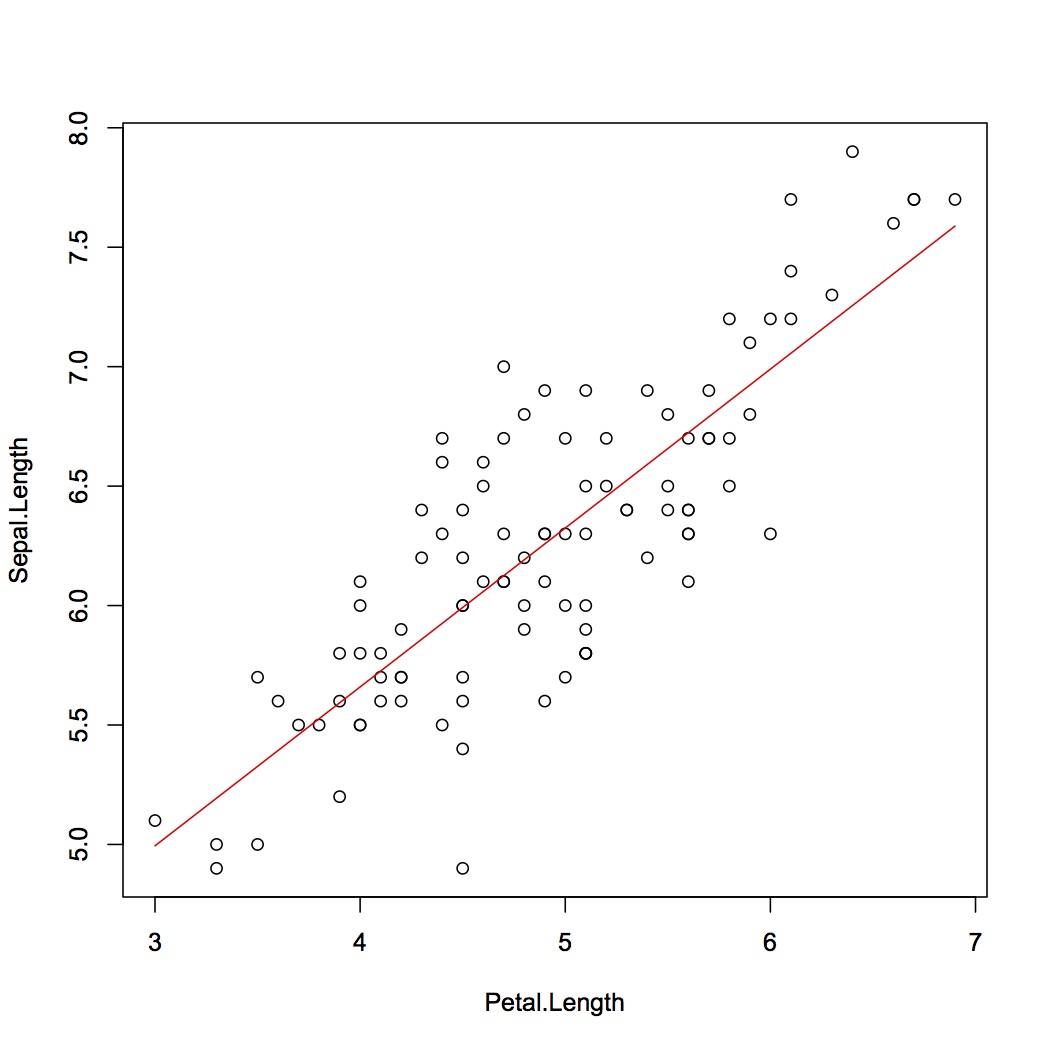
回帰分析の結果をプロットに重ね合わせる
> plot(Sepal.Length~Petal.Length, data=iris.new)
> lines(iris.new$Petal.Length,fitted(iris.mdl),col="red")